| 成绩一 | 成绩二... | ||
| 3 | ... | ||
| ... | ... | ||
| 24 | 刘丽 | 82 | 95 |
| 25 | ... | ||
| 26 | 陈伟 | ||
| ... | ... | ||
| 33 | 吴军 | ||
| ... | ... | ||
| 42 | 李秋梅 | ||
| ... | ... | ||
| 46 | 刘宏英 | ||
| ... | ... | ||
| 72 | 吴小艳 | ||
| ... | ... | ||
| 78 | ... |
如果两个同学分别叫 刘丽 刘兰,当加入刘兰时,地址24发生了冲突,我们可以以某种规律使用其它的存储位置,如果选择的一个其它位置仍有冲突,则再选下一个,直到找到没有冲突的位置。选择其它位置的方法有:
1、开放定址法
Hi=(H(key)+di) MOD m i=1,2,...,k(k<=m-1)
其中m为表长,di为增量序列
如果di值可能为1,2,3,...m-1,称线性探测再散列。
如果di取值可能为1,-1,2,-2,4,-4,9,-9,16,-16,...k*k,-k*k(k<=m/2)
称二次探测再散列。
如果di取值可能为伪随机数列。称伪随机探测再散列。
例:在长度为11的哈希表中已填有关键字分别为17,60,29的记录,现有第四个记录,其关键字为38,由哈希函数得到地址为5,若用线性探测再散列,如下:
0 1 2 3 4 5 6 7 8 9 10 60 17 29 (a)插入前
0 1 2 3 4 5 6 7 8 9 10 60 17 29 38 (b)线性探测再散列
0 1 2 3 4 5 6 7 8 9 10 60 17 29 (c)二次探测再散列
0 1 2 3 4 5 6 7 8 9 10 38 60 17 29 (d)伪随机探测再散列
伪随机数列为9,5,3,8,1...
2、再哈希法
当发生冲突时,使用第二个、第三个、哈希函数计算地址,直到无冲突时。缺点:计算时间增加。
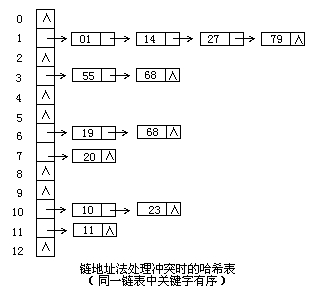
3、链地址法
将所有关键字为同义词的记录存储在同一线性链表中。
4、建立一个公共溢出区
假设哈希函数的值域为[0,m-1],则设向量HashTable[0..m-1]为基本表,另外设立存储空间向量OverTable[0..v]用以存储发生冲突的记录。