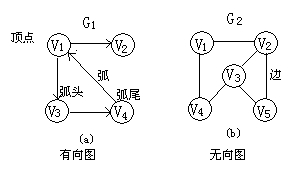
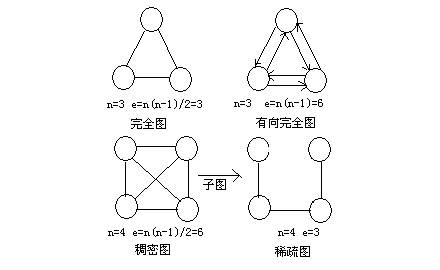
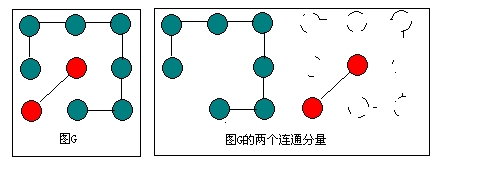
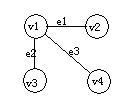
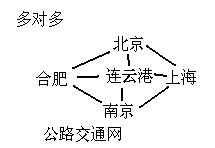
图是一种数据元素间为多对多关系的数据结构,加上一组基本操作构成的抽象数据类型。
ADT Graph{
数据对象V :V是具有相同特性的数据元素的集合,称为顶点集。
数据关系R:
R={VR}
VR={<v,w>|v,w(-V且P(v,w),<v,w>表示从v到w的弧,谓词P(v,w)定义了弧<v,w>的意义或信息}
基本操作P:
CreateGraph(&G,V,VR);
初始条件:V是图的顶点集,VR是图中弧的集合。
操作结果:按V和VR的定义构造图G
DestroyGraph(&G);
初始条件:图G存在
操作结果:销毁图G
LocateVex(G,u);
初始条件:图G存在,u一G中顶点有相同特征
操作结果:若G中存在顶点u, 则返回该顶点在图中位置;否则返回其它信息。
GetVex(G,v);
初始条件:图G存在,v是G中某个顶点
操作结果:返回v的值。
PutVex(&G,v,value);
初始条件:图G存在,v是G中某个顶点
操作结果:对v赋值value
FirstAdjVex(G,v);
初始条件:图G存在,v是G中某个顶点
操作结果:返回v的第一个邻接顶点。若顶点在G中没有邻接顶点,则返回“空”
NextAdjVex(G,v,w);
初始条件:图G存在,v是G中某个顶点,w是v的邻接顶点。
操作结果:返回v的(相对于w的)下一个邻接顶点。若w是v的最后一个邻接点,则返回“空”
InsertVex(&G,v);
初始条件:图G存在,v和图中顶点有相同特征
操作结果:在图G中增添新顶点v
DeleteVex(&G,v);
初始条件:图G存在,v是G中某个顶点
操作结果:删除G中顶点v及其相关的弧
InsertAcr(&G,v,w);
初始条件:图G存在,v和w是G中两个顶点
操作结果:在G中增添弧<v,w>,若G是无向的,则还增添对称弧<w,v>
DeleteArc(&G,v,w);
初始条件:图G存在,v和w是G中两个顶点
操作结果:在G中删除弧<v,w>,若G是无向的,则还删除对称弧<w,v>
DFSTraverser(G,v,Visit());
初始条件:图G存在,v是G中某个顶点,Visit是顶点的应用函数
操作结果:从顶点v起深度优先遍历图G,并对每个顶点调用函数Visit一次。一旦Visit()失败,则操作失败。
BFSTRaverse(G,v,Visit());
初始条件:图G存在,v是G中某个顶点,Visit是顶点的应用函数
操作结果:从顶点v起广度优先遍历图G,并对每个顶点调用函数Visit一次。一旦Visit()失败,则操作失败。
}ADT Graph