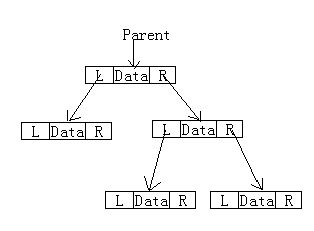
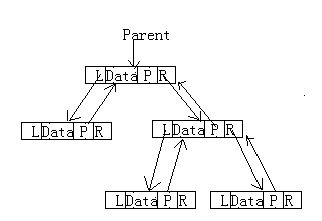
#define MAX_TREE_SIZE 100
typedef TElemType SqBiTree[MAX_TREE_SIZE];
SqBiTree bt;
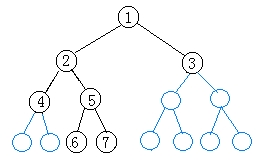
| 结点编号 |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
| 结点值 |
1
|
2
|
3
|
4
|
5
|
0
|
0
|
0
|
0
|
6
|
7
|
0
|
0
|
0
|
0
|
第i号结点的左右孩子一定保存在第2i及2i+1号单元中。
缺点:对非完全二叉树而言,浪费存储空间